¡No te vuelvas a confundir! El máximo común divisor no es lo mismo que el mínimo común múltiplo

El máximo común divisor (m.c.d.) es el número más grande que puede dividir dos o más cifras. En un primer momento, parece no tener ninguna utilidad, pero encontrar el máximo común divisor facilita la resolución de muchos problemas matemáticos y de otras ramas científicas. En este artículo, vamos a resolver cómo se halla el m.c.d. y qué usos nos ofrece este recurso. 

¿Para qué se utiliza el máximo común divisor?

Cómo hemos mencionado anteriormente, las matemáticas no son las únicas ciencias que emplean este recurso. La ingeniería o la física también utilizan el máximo común divisor. 

• Simplificar fracciones.

Algunas fracciones contienen números demasiado grandes para operar con ellos. Su reducción en cifras más pequeñas facilita la operacionalización con ellas. Para ello, es necesario encontrar el m.c.d. entre el numerador y el denominador; es decir, el mayor número que divida ambas cifras al mismo tiempo.

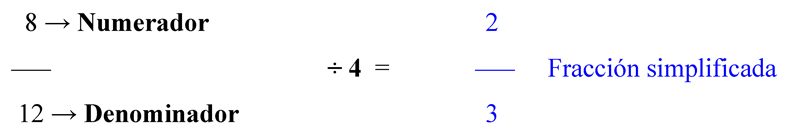
• Resolución de problemas aritméticos. 

Los problemas matemáticos aritméticos son aquellos que operan con cantidades numéricas. La aritmética básica se compone de operaciones simples (sumar, restar, multiplicar o dividir). El máximo común divisor se puede utilizar para problemas de división, pues permite agrupar cantidades. En el apartado Problemas para practicar, puedes probar a resolverlos. 

• Hallar el mínimo común múltiplo (m.c.m). 

El mínimo común múltiplo es otro recurso matemático que también tiene varias utilidades, al igual que el máximo común divisor. En el caso contrario al m.c.d., el mínimo común múltiplo es el número más pequeño como múltiplo en común dos o más números. El múltiplo es el resultado de la multiplicación de un número por otros. 

Para poder hallarlo a través del máximo común divisor se deben multiplicar las cifras numéricas escogidas. Una vez resuelta dicha operación, se divide por el m.c.d. y el resultado será el mínimo común múltiplo. Pongamos un ejemplo para facilitar la comprensión de este procedimiento. 

m.c.d. (8, 12) = 4 → 8 ✕ 12 = 96 

96 ÷ 4 = 24 (m.c.m)

Si comprobamos cuál es el mínimo común múltiplo de 8 y 12, el resultado es 24. 

Múltiplos de 8 = 8 (8 ✕ 1), 16 (8 ✕ 2), 24, 32…

Múltiplos de 12 = 12 (12 ✕ 1), 24 (12 ✕ 2), 36, 48…

• Física e ingeniería: calibrar instrumentos. 

El máximo común divisor no es un procedimiento exclusivamente para las matemáticas. También se emplea en otras ciencias, como la física o la ingeniería. En la calibración de instrumentos, el máximo común divisor permite obtener mediciones exactas entre las unidades de medida empleadas.

Cómo se calcula el máximo común divisor

El procedimiento para hallar el máximo común divisor de dos o más cifras numéricas es descomponerlas en factores primos. Los factores primos son aquellos números que solo pueden dividirse entre 1 y él mismo. Por ejemplo, el número 2 tiene como divisores el 1 y el 2. Hagamos el cálculo paso a paso. 

1. Descomponer en factores primos.En este ejemplo utilizaremos tres cifras en lugar de dos. Los números serán 8, 28 y 40. 8=2·2·2=2³ / 28=2·2·7=2²·7 / 40=2·2·2·5 =2³·5
2. Escoger los números comunes.Una vez descompuestas las cifras en factores primos, seleccionamos los que tengan en común. En el caso de que hayan factores primos que se repitan, escogemos la cantidad que tengan las tres cifras en común; es decir, la potencia con el índice más pequeño. 8=2·2·2=2³ / 28=2·2·7= 2²·7 / 40=2·2·2·5=2³·5
3. Multiplicar los números comunes.Finalmente, el último paso sería la multiplicación de los factores primos que tengan en común las cifras para hallar el máximo común divisor. 2·2 = 2² = 4

Ejercicios para practicar

Ahora que ya sabes cómo se resuelve el máximo común divisor, te dejamos algunos ejercicios para que puedas practicar. 

• Ejercicio 1: Calcula el máximo común divisor de estas series de números.

m.c.d. (18, 81) = m.c.d. (14, 120) =

m.c.d. (300, 530) = m.c.d. (305, 340) =

m.c.d. (16, 40, 404) = m.c.d. (32, 58, 62) = 

• Ejercicio 2: Si el máximo común divisor de 125 y 60 es 5, ¿cuál es su mínimo común múltiplo? 
• Ejercicio 3: PROBLEMA: María ha ido al centro con su madre para comprar varios paquetes de manzanas y peras. En el paquete de manzanas hay 69 unidades. En el paquete de peras hay 15 unidades. La madre de María le ha pedido a su hija que meta en una bolsa el máximo número de peras y manzanas para dárselas a su abuela. La única condición que le pide es que haya el mismo número de peras y manzanas. ¿Cuántas manzanas y peras debe meter María en la bolsa para que haya el mismo número, tanto de peras como de manzanas?

Con la lectura de este artículo y la práctica de los ejercicios propuestos, dominarás el cálculo del máximo común divisor en un santiamén. Te dejamos algunos artículos relacionados para que practiques más recursos matemáticos. Coméntanos si te ha servido, y si conocías la técnica para hallar el m.c.d. ¡Os leemos!