La regla de tres: el secreto matemático que usamos sin saberlo
La regla de tres se utiliza para encontrar un valor desconocido en una relación proporcional entre tres valores conocidos. Es aplicable en situaciones tan variadas como:
- Conversión de monedas y unidades.
- Cálculos de porcentajes, descuentos o aumentos.
- Escalado de planos o mapas.
- Variación de cantidades en recetas de cocina.
- Análisis de velocidad, tiempo y distancia.
- Resolución de problemas de economía doméstica y comercio.
Hay dos tipos de regla de tres:
- Directa: cuando al aumentar una magnitud, la otra también aumenta (o ambas disminuyen).
- Inversa: cuando al aumentar una magnitud, la otra disminuye, y viceversa.
Veamos primero los pasos para la regla de tres directa:
- Identificar las magnitudes relacionadas y clasificar cuál es conocida y cuál es la que se desea encontrar.
- Colocar las cantidades en forma de proporción:
Si A está relacionado con B, y C con un valor X (desconocido), entonces:
A → B
C → X - Aplicar la fórmula: se multiplican las variables “en forma de cruz.
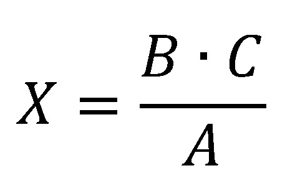
Para la regla de tres inversa: se multiplican “en línea”.
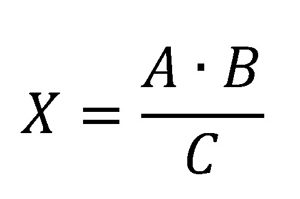
Ejemplo 1 – Regla de tres directa
Si 3 cuadernos cuestan 9€, ¿Cuánto costarán 5 cuadernos?
3 cuadernos →9€
5 cuadernos → X€
Respuesta: 5 cuadernos costarán 15€.
Ejemplo 2 – Regla de tres inversa
Si 4 obreros terminan una obra en 6 días, ¿Cuántos días necesitarán 3 obreros?
4 obreros →6 días
3 obreros → X días
Respuesta: 3 obreros necesitarán 8 días.
- Si 8 lápices cuestan 64 céntimos, ¿cuánto costarán 5 lápices?
- Una máquina produce 120 piezas en 4 horas. ¿Cuántas piezas producirá en 7 horas?
- Si 6 personas limpian un salón en 3 horas, ¿Cuánto tardarán 4 personas?
- Si con 2 litros de pintura se cubren 10 m², ¿Cuántos m² se cubrirán con 5 litros?
(Respuestas al final del artículo)
La regla de tres no es solo un método práctico; es una oportunidad para enseñar a nuestros estudiantes a razonar proporcionalmente, a vincular el pensamiento matemático con la vida diaria y a ver en los números algo más que operaciones.
Los ejemplos de la vida cotidiana, como los que hemos visto en este artículo, son una excelente manera de enseñar y aprender la regla de tres. ¿Qué técnicas o métodos han sido útiles para enseñar estos conceptos en el aula? ¡Nos encantaría conocerlos!
Respuestas a los ejercicios para practicar:
Ejercicio 1: se trata de una regla de tres directa (menos lápices, menos dinero)
- 8 lápices → 64 céntimos
- 5 lápices → X céntimos
Solución: 5 lápices cuestan 40 céntimos.
Ejercicio 2: es una regla de tres directa (más tiempo, más piezas):
- 4 horas → 120 piezas
- 7 horas → X piezas
Solución: En 7 horas producirá 210 piezas.
Ejercicio 3: se trata de una regla de tres inversa (menos personas, más tiempo):
- 6 personas → 3 horas
- 4 personas → X horas
Solución: 4 personas tardarán 4 horas y media (4 horas y 30 minutos).
Ejercicio 4: Es una regla de tres directa (más pintura, más superficie):
- 2 litros → 10 m²
- 5 litros → X m²
Respuesta: Con 5 litros se cubrirán 25 m².






Utilizando la regla de tres ayudamos a los alumnos a fomentar el análisis lógico, la organización de datos y la resolución rápida de problemas. La regla de tres nos permite pensar de forma lógica y eficiente. Está muy bien este artículo porque nos recuerda la utilidad y la importancia de la regla de tres.
Con la regla de tres fomentamos el cálculo mental en los alumnos, tan necesario para distintos campos en la vida diaria.
Con la regla de tres ayudamos a los alumnos a la organización de datos, la resolución rápida de problemas y el análisis lógico.
Ahora que estamos en verano, la regla de tres nos viene muy bien para los viajes y la planificación, cómo estimar el tiempo del viaje, calcular gastos compartidos entre amigos, etc. Por ejemplo: si recorres 97 km en 2 horas, ¿cuánto tardarás en recorrer 497 km?