Cómo hacer de las derivadas una herramienta didáctica con sentido
Las derivadas tienen múltiples usos en la vida real. Por ejemplo, sirven para prever el cambio de temperatura o la llegada de una tormenta. © ADOBE STOCK
En esencia, la derivada de una función mide su tasa de cambio en un punto. Es decir, nos dice cómo varía una magnitud respecto a otra. Si una función representa la posición de un coche en función del tiempo, su derivada nos da la velocidad en cada instante. Si representa la temperatura de una ciudad a lo largo del día, su derivada nos informa de si está subiendo o bajando la temperatura y a qué ritmo.
A la hora de enseñar derivadas en Secundaria o Bachillerato, conviene identificar aquellas que forman parte del repertorio básico que los estudiantes deben memorizar y comprender:
Derivada de una constante (k):
Derivada de una potencia:
Derivada de funciones trigonométricas:
Derivada de funciones exponenciales y logarítmicas:
Estas derivadas son las “tablas de multiplicar” del cálculo diferencial: sin ellas, es imposible avanzar.
Aparte de aprender las derivadas elementales, nuestros alumnos deben manejar una serie de técnicas que permiten derivar funciones más complejas:
Regla de la suma:
(f(x)+g(x))´=f´(x)+g´(x)
Regla del producto:
Regla del cociente:
Regla de la cadena:
Estas técnicas permiten descomponer funciones complejas en piezas manejables y derivarlas de forma ordenada.
Una pregunta habitual en clase es: “¿Y esto para qué sirve?”. Las derivadas permiten optimizar, predecir, controlar y modelizar fenómenos. Algunos ejemplos concretos que podemos proponer en clase:
- Economía: determinar el máximo beneficio o mínimo coste.
- Medicina: calcular la velocidad de propagación de un virus o la dosis óptima de un medicamento.
- Ingeniería: modelar la resistencia de materiales y el diseño aerodinámico.
- Deportes: analizar la trayectoria de un balón o el ritmo cardíaco de un atleta.
- Meteorología: prever el cambio de temperatura o la llegada de una tormenta.
Las derivadas son mucho más que una operación algebraica: son una herramienta esencial para entender, predecir y optimizar la realidad.
Porque, al fin y al cabo, vivimos en un mundo que cambia constantemente, y las derivadas son la clave para comprender ese cambio.
¿Qué recursos han sido interesantes en tus clases de derivadas?, ¿qué técnicas te han resultado útiles para enseñar este concepto? ¡Cuéntanoslas en los comentarios!



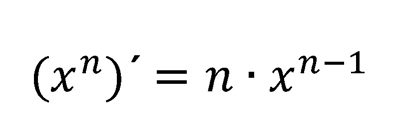
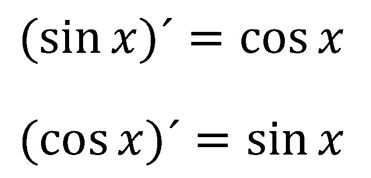
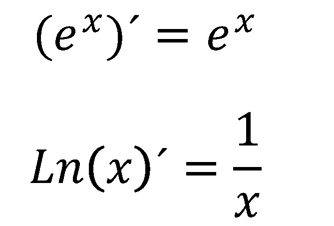
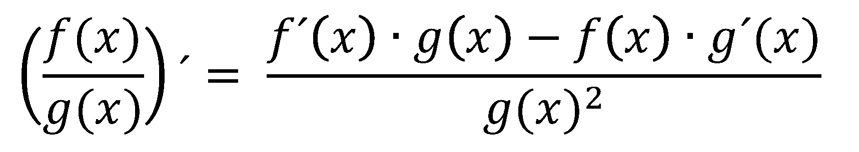



Me gusta el enfoque del artículo, algo tan complejo como puede ser derivar con fórmulas básicas y sencillas relacionadas con la vida real. Enhorabuena a la autora por el artículo!
Qué momento más oportuno de publicar este artículo, pues en estos días de tanto calor, estamos todos viendo el tiempo qué tendremos y la predicción para los próximos días. Esperamos con alegría la bajada de la temperatura y para obtener esta información tan necesaria en verano, se usan las derivadas (prevén el cambio de temperatura y el ritmo) por tanto, cómo dices en el artículo las derivadas se utilizan en muchos campos de la vida diaria, nos facilitan la vida y nos ayudan a tomar decisiones.
En el campo sanitario, las derivadas ayudan a evitar riesgos y procesos infecciosos; por ejemplo los
modelos matemáticos de propagación de infecciones, como los modelos SIR (Susceptible-Infectado-Recuperado), usan derivadas para calcular tasas de infección y recuperación.